| 96 kHz.org |
| Advanced Audio Recording |
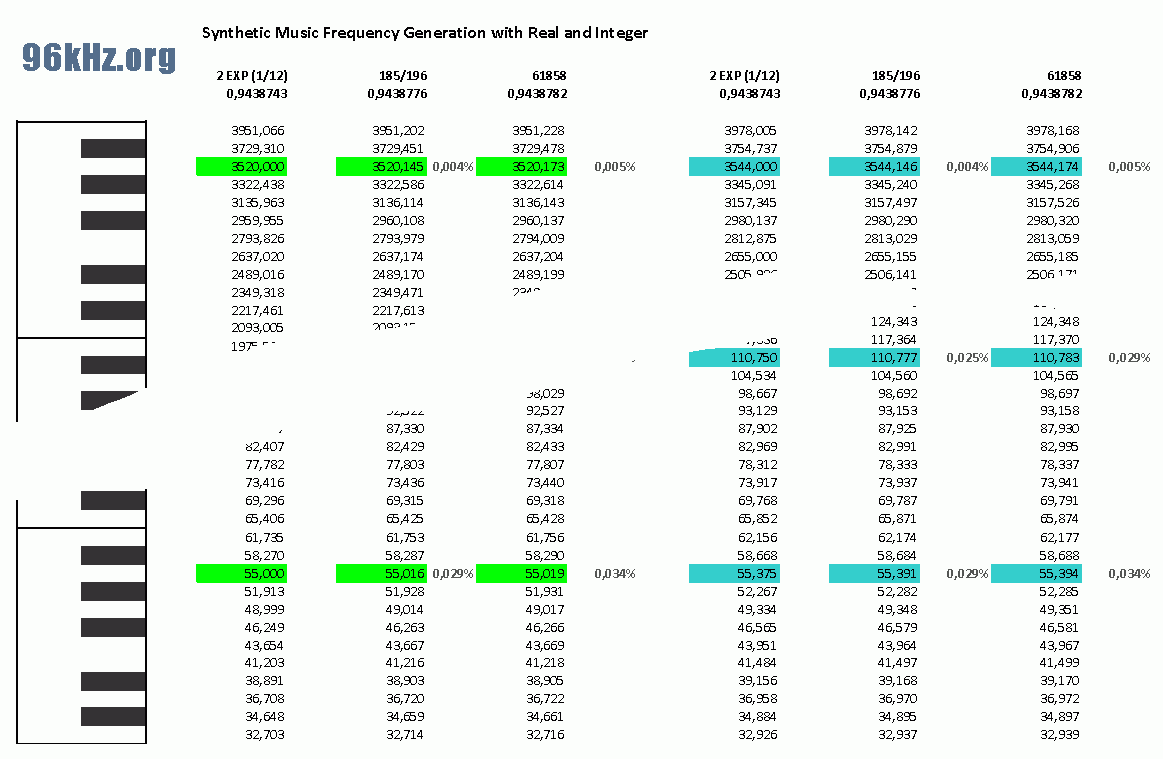
Generation of Music Frequencies with DSPs This idea shows a concept how to create frequencies in balanced (tempered) tuning with a precision of better than 0,04% over 9 octaves and 0,005% within one octave with just one starting value and simple iterative multiplication using a fixed number. This makes it possible to calculate all of them in real time without having an exponential function included in the DSP. It is an improved version of my first approach with the "magic relation" using the numbers 196/185 in my first audio synthesizer applications with the Commodore 64.
The magic number Unlike with many acoustic instruments which use pure tuning, the notes of several instruments like most keyboards, pianos and synthesizers are setup with equidistant balanced tuning to meet all music tunes / keys. From the theory this tuning can be achieved by multiplying / dividing the frequency of an adjacent note by 2 EXP(1/12) which is around 1,05946309. Searching for an easy representation of this irrational number in the Integer number system, I was pleased to find the magic numbers of 196/185 which is 1,0594594 and nearly perfectly meet this value, however. It is that precise (better than 4ppm) that the accumulated error over an octave is less than 0,005 % and so it can be used recursively even over several octaves. The error all over is inferior to the typical rounding problems of the subsequent calculations in music synthesis chains. It should be applied to float and high precision INT calculations. In other cases a common INT multiplication can be used with the number 61858 in binary representation of 16 Bits.
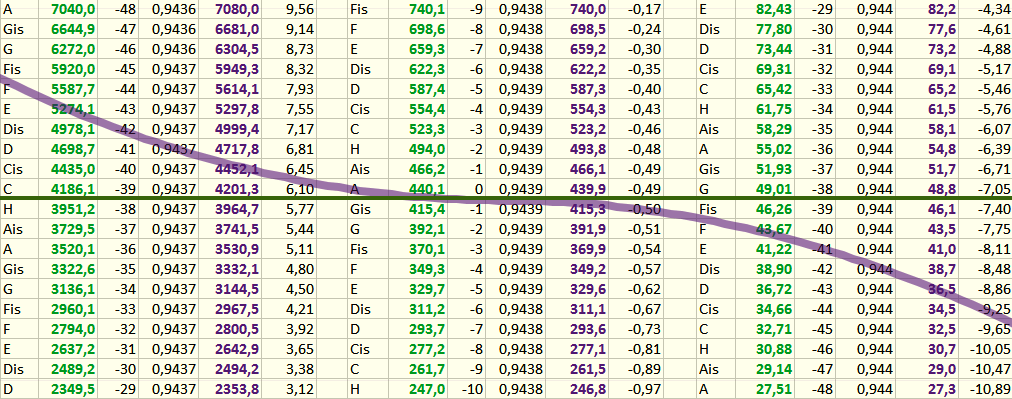
full frequency table synthesis The following table shows the highest and lowest frequencies of a theoretical piano setup with all of the audible sine frequencies for both the nominal chamber tone of 440Hz and the real tone for classical orchestras of 443Hz. Starting from 16 x the chamber note 7040Hz and 7088Hz, the multiplication is permanently repeated down to the lowest frequencies for all 3 cases.
The final error is surprisingly small and can even be lowered by restarting the calculation for each octave at e.g. the A key 880Hz, 440Hz, 220Hz and so on. For DSPs without real support, the right column shows the result for iterative application of the binary division using 61858 / 65536. In most cases, division is recommend starting from the high frequent tones rather than running up the table and perform multiplication.
Variations To meet the requirement of a perfect tuning over the octave range of perform a detuning to generation piano like frequency spreading a factor can be added this way: f(t+1) = f(t) * (61858 +/- x) / 65536 where x controls positive and negative spreading.
Conclusion A complete set of music frequencies for balanced tuning can be generated with DSPs at runtime by iteration using simple number relations. For the mostly used frequencies with synthetic sound generation in between 30Hz and 3kHz, the error stays below 0,04% for full sequential processing.
|
| © 2000 - Jürgen Schuhmacher |